Compressibility Factor For Air on HP50g

     The compression factor is related to the difference between the behavior of real and ideal gases. The ideal gas model tends to fail at low temperatures or high pressures, requiring correction. In the image below is shown an example of this misbehavior, in the case for nitrogen.

 Source: http://www.chem.ufl.edu/~itl/4411/lectures/lec_e.html

The compressibility factor is expressed by the relationship:

     There are several methods for finding the compressibility factor under certain conditions of pressure and temperature. The classic method is to search for the information on diagrams available in the relevant literature, but here is shown another method that is based on a modification of the Redlich-Kwong equation of state. It is an iterative method.

      The algorithm shown is proposed by Tapan Kumar Sen and published by Breno Tresoldi Minzon and Fabio Malavazzi Santilio. The original program, that operates in Reverse Polish Notation (RPN), is available in http://www.hpcalc.org/details.php?id=5806.

     The proposed approach is iterative, making an interesting use of programmable computers. The method is to guess an initial value for "Z" and iteratively achieve convergence between the following formulas:

 

 

 

  

Pr is the reduced pressure, given by Pr equals  P / Pc.
Tr is the reduced temperature, given by Tr equals T / Tc.

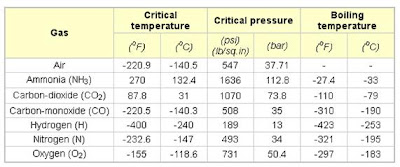
      The constant Pc and Tc are the critical pressure and the critical temperature of the gas. The values for some gases are shown in the table below.

 

Source: http://www.engineeringtoolbox.com/gas-critical-temperature-pressure-d_161.html

     As my interest lies in the properties of air (applied to compressors, internal combustion engines) the code shown is built to deal directly with this gas.

    The following example is in USER RPL, to use with HP50g calculator in Algebraic mode.

The program also can be downloaded here.

Thanks for reading.

Eddie